각의 n의 일반화를 잘못했슴을 발견하였습니다.
n 등분은 이미 증명된 2등분의 배수나 3등분의 배수는 당연히 등분이 될 것이고, 3등분 이상의 소수에 대한 등분의 가능성을 검토하는 것이 필요할 것입니다.
위 그림처럼 5등분을 검토하여 가능함을 확인 하였고, 아래와 같이 7등분과 9등분, 13등분에 대하여 같은 방법을 시행하여 성립함을 확인하였습니다.
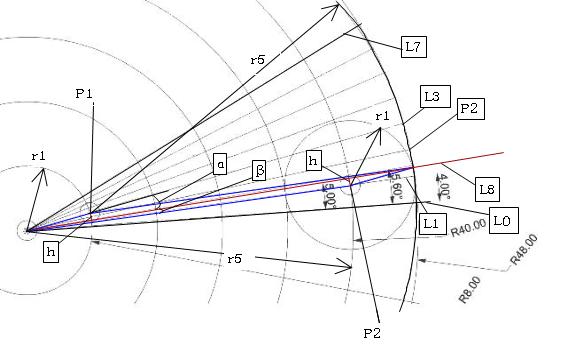
위의 그림은 주어진 각도(L0-0-L7)이 28도(4도*7=28도)의 각일 때, 28도 각을 5등분하는 방법을 보인 것입니다.
앞의 글에서는 주어진 각을 반지름을 5등분하고 내각에 대하여는 5+3= 8등분하여 반지름*내각을 5*8로 등분을 시행한 다음에, 첫 번째 각의 선분(L1)의 5번째(r5) 등분점(P2)에 원호(r1)의 반지름을 그리고, 네 번째 각의 선분(L4)에 5번째 원호의 반지름(r5)을 그려서 만나는 점(P3)에서 원호의 중심인 원점 0에 연결하여 L8을 얻은 것입니다.
L8은 28도를 5등분하는지 확인하기 위하여 얻은 선분입니다.
이 그림에 대하여 앞에 3등분을 증명한 방식을 적용하여 검토하면, 청색으로 그린 원점0-P2와 P1-P3의 선분은 반지름 r5의 길이이고, 원점0-P1과 P2-P3는 R1의 반지름과 같은 길이입니다. 이로서, 청색의 선들은 평행사변형의 모양이 됩니다.
적색으로 표시된 L8에 P1과 P2에서 각각 수선을 내리고, 그 선분을 h로 표시합니다.
그러면 주어진 각을 5등분한 L3-L2각을 나누고 있는 L8직선의 상부의 각을 α라 하고, 하부의 각을 β라고 하면, 수식은 아래와 같이 됩니다.
α= asin(h/1r), β=asin(h/5r) 가 됩니다.
따라서,
α : β = asin(h/1r) : asin(h/5r) = 5: 1이 되어야 계산상으로는 5등분을 만족하게 됩니다.
그러나, 앞의 글에서 보았듯이 만족하지 못합니다. α : β = asin(h/1r) : asin(h/5r) 가 아니었습니다.
그래서 주어진 각에 대하여 asin(h/1r)와 각(h/1r)의 보정값인 r5 대신에 r5+λ를 적용할 필요가 있습니다.
삼각함수표에 각도와 asin 값사이의 오차에 보정할 수 있는 반지름 r에 대한 보정값 λ표를 만들어 사용하면 될 것입니다.
그래서 아래와 같이, 5등분, 7등분, 9등분, 13등분에 대하여 보정값 r5+λ을 적용한 그림을 그렸습니다.
이렇게 하면, 오차가 없는 작도가 될 것입니다.
앞의 5등분의 방식을 n 등분에 적용하면,
주어진 각을 n 등분을 하려고 하는 경우에, 반지름에 대하여 n등분을 하고, 내각에 대해서는 n+3등분을 합니다. 그래서 반지름*내각을 n*n+3으로 등분을 시행한 다음에, 첫 번째 각의 선분(L1)의 n번째(rn) 등분점(P2)에 원호(r1)의 반지름을 그리고, 네 번째 각의 선분(L4)에 n번째 원호의 반지름(r5)에 보정값 λ을더한 n+ λ의 반지름을 그려서 만나는 점(P3)에서 원호의 중심인 원점 0에 연결하여 Ln+3의 선분을 얻은 것입니다.
직선 Ln+3은 주어진 각을 n등분하는 선분입니다.
청색으로 그린 원점0-P2와 P1-P3의 선분은 반지름 rn+λ의 길이이고, 원점0-P1과 P2-P3는 R1의 반지름과 같은 길이입니다. 이로서, 청색의 선들은 평행사변형의 모양이 됩니다.
이렇게 얻은 P3와 원점을 이은 직선이 주어진 각을 n 등분하는 선이 됩니다.
n배수 λ보정표를 만들어서 사용하기는 곤란하고, 좀더 정밀한 등분이 필요하면, 한번더 4등분 또는 n+2 등분을 하면 되고, 아니면, 한번더, 그러나 무한등분까지 가지 않아도, 1-3 번 이내로 더 분할하는 것으로 미분에서 sinx/x의 미분을 1로 보는 상태와 같은 상태가 될 것입니다. 사실상 10등분이하에서는 각의 차이가 크지만, 10 등분 이상은 분할 각이 그림에서 보는 것처럼 바늘처럼 예각이고, 20 등분 이상에서는 더더욱 그림상에 미세한 각이 되는 것입니다. 즉 일반각에서는 10 등분이상에서는 sinx와 각고 x를 같이 보는데 무리가 없다는 것입니다.
반대의견이 예상되지만, 각의 삼등분의 난제는 대수학 문제가 아니고, 작도문제일 것입니다.
나침반이 정북을 가르치지 않아도 우리가 나침반을 써야 하고, 원주율π의 정확한 값을 몰라도 원주의 길이를 계산해야 합니다. sinα: sinβ와 각도 α: β의 비율이 근소하게 다른 것이 이것과 다르지 안하다고 본다면, 나의 방법이 각의 3등분, n 등분으로 인정할만 한 것인지 묻고 싶습니다. 이 난제는 작도를 요구하는 것이고, 근본 취지는 정확한 계산값을 요구하기 보다는 작도의 논리의 정합성일 것이기 때문입니다.
<5등분의 예>
<각의 7등분의 예>
<각의 9등분의 예>
<각의 13등분의 예>
3 등분은 앞에 본 바와 같이 5등분 이상의 n등분과는 방법상에 다릅니다.
앞에 소개했던 방법에 대하여 반지름 r4에 반지름 r4+λ를 적용한 그림을 아래와 같이 첨부 합니다.
<각도의 3등분의 예>
벡터에서 합력을 구하는 평행사변형의 방법과 각도의 3 등법을 적용한 것입니다.
아래 그림은 힘이 3 :1인 경우를 본 것입니다.
만약 힘이 5 :1인 경우는 5:1 등분법으로 해야 한다는 생각입니다.
즉, 힘이 n :1이면 n : 1 등분법을 사용해야 한다는 생각입니다.
아래의 그림에서,
검은색 점선은 두 개의 힘을 나타낸 것이고,
청색 굵은 선은 기존의 평행사변형 법으로 본 것이고,
적색 굵은 선은 3 :1 등분선에서 평행사변형을 적용한 것입니다.
물리적으로 어떤 방법이 옳은지 생각해 볼 필요가 있는 것 같습니다.